Coherent Pion Production - Thesis

4. Coherent Pion Production

A coherent neutrino-nucleus interaction, as introduced in Section 3.6.1, is defined as one which leaves the nucleus in the same quantum state as it was initially. The nucleus' constituents must retain their identity, and the nucleus cannot be excited or fragmented, though it can recoil.

A specific case of this type of interaction is that of coherent pion production, which can procede either via the charged- or neutral-current, and in which the neutrino scatters off the nucleus, A, and produces a single pion of appropriate charge:

ν_l A → l^- π⁺ A
ν_l A → l⁺ π^- A
ν_l A → ν_l π⁰ A

Coherent pion production has become an important interaction to neutrino physics for two reasons. First, the neutral-current channel results in the production of a single π⁰ with no other observable particles. Since π⁰'s exclusively decay to two photons, any decay where the photons are collinear or one of the photons has most of the energy in the laboratory-frame, runs the risk of being mis-identified as an electron. This makes coherent π⁰ production a dangerous background for oscillation experiments searching for ν_e. Second, coherent pion production is an important part of the broader goal of understanding neutrino-induced pion production in general. Due to the nuclear effects discussed in Section 3.6, it is quite possible for CC QE interactions to produce an outgoing pion, and similarly possible for a pion-producing interaction to have the pion absorbed. Correctly understanding coherent pion production therefore is a necessary part of any effort to improve understanding of these other reactions.

The requirement that the nucleus remain intact and unaffected by this interaction gives rise to several characteristic features of coherent pion production. The first is that the four-momentum transferred to the nucleus must remain small, since any substantial transfer absorbed by the nucleus would excite or otherwise fragment it and break coherence. This is characterised by the kinematic variable, |t|, which is the squared four-momentum transfer to the nucleus, from the neutrino-lepton-pion system:

|t| = |{(q - P_{π})}^{2}| = |{(P_{ν} - P_{l} - P_{π})}^{2}|

(4.1)

Figure 4.1 shows |t| in relation to the other momentum transfers in the conventional view of CC coherent pion production. Of all the kinematic variables, |t| is the most characteristic indicator of coherence. The usual measure of momentum transfer, Q², is at times used in its stead but since larger transfers to the pion do not in principle break coherence it is not as direct an indicator.

Figure 4.1: The conventional view used to describe coherent pion production, shown for the ν_μ CC case. The squared four-momentum transfer to the nucleus is denoted |t|.

As a result of requiring small momentum transfers, coherent pion interactions also tend to produce events with a very forward-going lepton and pion with respect to the incoming neutrino's direction. In the case of NC coherent this is particularly useful, since the inability to observe the final-state lepton prevents the calculation of |t|. Finally, because the nucleus remains intact and recoils only slightly, coherent pion production is often distinguished by searching for additional short tracks or large energy deposits at the interaction vertex, the presence of either hinting at a non-coherent interaction.

4.1. Experimental History

The first observation of coherent pion production was reported in February 1983 by the Aachen-Padova spark-chamber experiment [1] in CERN's PS neutrino/anti-neutrino beam. While studying a sample of solitary π⁰s produced in their ν_μ and ν_μ beams they observed a significant excess of events in the forward-going direction, an excess that was not present in another sample in which the π⁰ was produced along with a proton (Figure 4.2). They identified this excess as NC coherent pion production: a theoretical description of which had first been published by K.S. Lackner [2] four years earlier in the context of determining the structure of the weak neutral-current.

Figure 4.2: The data (histogram) and theoretical prediction (curve) for the angular distribution of π⁰s produced in Aachen-Padova's ν_μ (left) and ν_μ (right) beams. The solid lines represent a sample of isolated (“naked”) π⁰s, and the dashed lines a sample where the π⁰ is accompanied by a recoil proton. There is a clear excess in the “naked” sample in the forward-going region [1].

In response to Aachen-Padova's discovery, Dieter Rein and Lalit Sehgal developed a theoretical model for coherent pion production [3], building on Lackner's paper and their own recent work on resonance pion production. Their predictions agreed with the cross-section extracted by Aachen-Padova, as well as one from a retrospective re-analysis of data from the Gargamelle experiment [4].

Over the following decade five more experiments observed and measured both CC and NC coherent pion production with neutrinos and anti-neutrinos. Many giving exceptionally clean and clear signals of coherent production such as those in Figure 4.3. Over a wide range of neutrino energies all experimental data were consistent with predictions from the Rein-Sehgal model, within the resolution of the measurements (Figure 4.4).

Figure 4.3: Clear CC coherent signals in |t| measurements. (Left) The the BEBC [5] experiment's bubble chamber detector had excellent resolution on additional short tracks, “stubs”, at the vertex. (Right) The CHARM II [6] experiment took high statistics data with a clear and well described coherent (white) component.

Figure 4.4: The cross-section for CC (top) and NC (bottom) coherent pion production on ²⁷Al. The data are all experimental measurements from ν_μ and ν_μ with E_ν ≥ 2 GeV. They are compared with the Rein-Sehgal predictions from GENIE and NEUT. The data and NEUT are scaled to ²⁷Al according to the approximate A^⅓ dependancy noted by Rein-Sehgal.

The resurgence of neutrino physics that accompanied the discovery of oscillations at the beginning of the 21st century also brought about a series of experiments at lower neutrino energies than had been studied previously. In stark contrast to previous experiments, K2K's search for CC coherent pion production at E_ν of 1.3 GeV found no evidence for its existence. This surprising result was later confirmed by SciBooNE, which also set cross-section limits well below the level predicted by the Rein-Sehgal model implemented in NEUT (the interaction simulation both experiments were using), shown in Figure 4.5. Measurements of NC coherent pion production were successfully made in both MiniBooNE and SciBooNE, but even here the cross-sections reported were a substantial reduction on the values expected from the Rein-Sehgal implementations in NEUT and NUANCE.

Figure 4.5: The 90% CL limits set for CC coherent pion production on ¹²C by the K2K and SciBooNE experiments. Compared with Rein-Sehgal from NEUT and GENIE. The width of the SciBooNE limits is the RMS of the interacting neutrinos in the respective sample. The energy range of the K2K result is unpublished.

Table 4.1 lists all experimental data on neutrino induced coherent pion production. With measurements in multiple beamlines, on multiple targets, and across a range of neutrino energies, the experimental evidence for the existence of coherent pion production is clear and undeniable. But below neutrino energies of ∼2 GeV the previously successful Rein-Sehgal model over-predicts the NC cross-section, and there is no experimental evidence for CC coherent production at all.

Table 4.1: A summary of all experimental data on neutrino induced coherent pion production. The E_ν stated is the flux average, with the exception of MiniBooNE for which it is the flux peak, and Gargamelle which is an estimate. The values of A^eff are the best estimates available and are the ones used to scale the data in Figure 4.4.
Experiment	Target (A^eff)	E_ν [GeV]	Reac.	Cross-Section [10^-40cm²/nucleus]	Ref
Aachen-Padova	Aluminium (27)	2	NC ν_μ	29 ± 10	[1]
Aachen-Padova	Aluminium (27)	2	NC ν_μ	25 ± 7	[1]
Gargamelle	Freon (30)	3.5	NC ν_μ	31 ± 20	[4]
Gargamelle	Freon (30)	3.5	NC ν_μ	45 ± 24	[4]
CHARM	Marble (20)	31	NC ν_μ	96 ± 42	[7]
CHARM	Marble (20)	24	NC ν_μ	79 ± 26	[7]
SKAT	Freon (30)	7	NC ν_μ	52 ± 19	[8]
SKAT	Freon (30)	7	CC ν_μ	106 ± 16	[8]
SKAT	Freon (30)	7	CC ν_μ	113 ± 35	[8]
BEBC	Neon (20)	27	CC ν_μ	175 ± 25	[5]
BEBC	Neon (20)	27	CC ν_μ	250 ± 49	[9]
FNAL E632	Neon (20)	91.1	CC ν_μ	350 ± 80	[10]
FNAL E632	Neon (20)	74.5	CC ν_μ	270 ± 110	[10]
CHARM II	Glass (20.7)	23.7	CC ν_μ	168 ± 41	[6]
CHARM II	Glass (20.7)	19.1	CC ν_μ	161 ± 40	[6]
K2K	Carbon (12)	1.3	CC ν_μ	< 0.077 (90% CL)	[11]
MiniBooNE	CH₂ (12)	0.7	NC ν_μ	(0.195 ± 0.075) × σ_NCπ⁰	[12]
SciBooNE	Carbon (12)	1.1	CC ν_μ	< 0.0844 (90% CL)	[13]
SciBooNE	Carbon (12)	2.2	CC ν_μ	< 0.287 (90% CL)	[13]
NOMAD	Carbon (12.8)	25	NC ν_μ	72.6 ± 10.6	[14]
SciBooNE	Carbon (12)	0.8	NC ν_μ	(0.012 ± 0.002) × σ_CC	[15]

4.2. Rein-Sehgal Model

As mentioned above, the majority of data on coherent pion production, taken at high neutrino-energies, is satisfactorily described by the model published by Deiter Rein and Lalit Sehgal [3] and updated to account for a non-zero final-state lepton mass [16].

The Rein-Sehgal model begins from Adler's partially conserved axial-vector current (PCAC) theorem [17], which allows the cross-section for neutrino-nucleus scattering to be described in terms of the analogous pion-nucleus interaction. This is then adapted to the specific case of coherent pion production, and modified to account for the reduction of that cross-section due to the potential for intra-nuclear pion absorption (which would break coherence). In the final part of Rein-Sehgal, choices for the various inputs to the model are made, some of which can have noticeable effects on both the total and differential cross-sections predicted.

All the cross-section plots shown in this section were calculated using GENIE version 2.6.6, which was modified to fix a bug in the calculation of the pion-nucleon cross-sections which are an input to the Rein-Sehgal model.

4.2.1. Adler's PCAC Theorem

The general approach of Adler's PCAC theorem [17] can be broken into two steps. First, it is found that in the limit of small-angle scattering, where the final-state lepton is parallel to the incoming neutrino, the cross-section for neutrino-nucleus scattering depends only on the divergence of the axial-vector part of the weak current. Second, as a consequence of PCAC, the divergence of the axial-vector current can be related to the pion.

Effectively then, when the final-state lepton's scattering angle is small, the cross-section for weak scattering from an initial hadronic system, α, to a final hadronic system, β can be related to the analogous process in pion scattering, as shown in Figure 4.6.

Figure 4.6: Adler's PCAC theorem relates the amplitude for ν_l α → l β (left) to the analogous process for pion scattering π α → β (right).

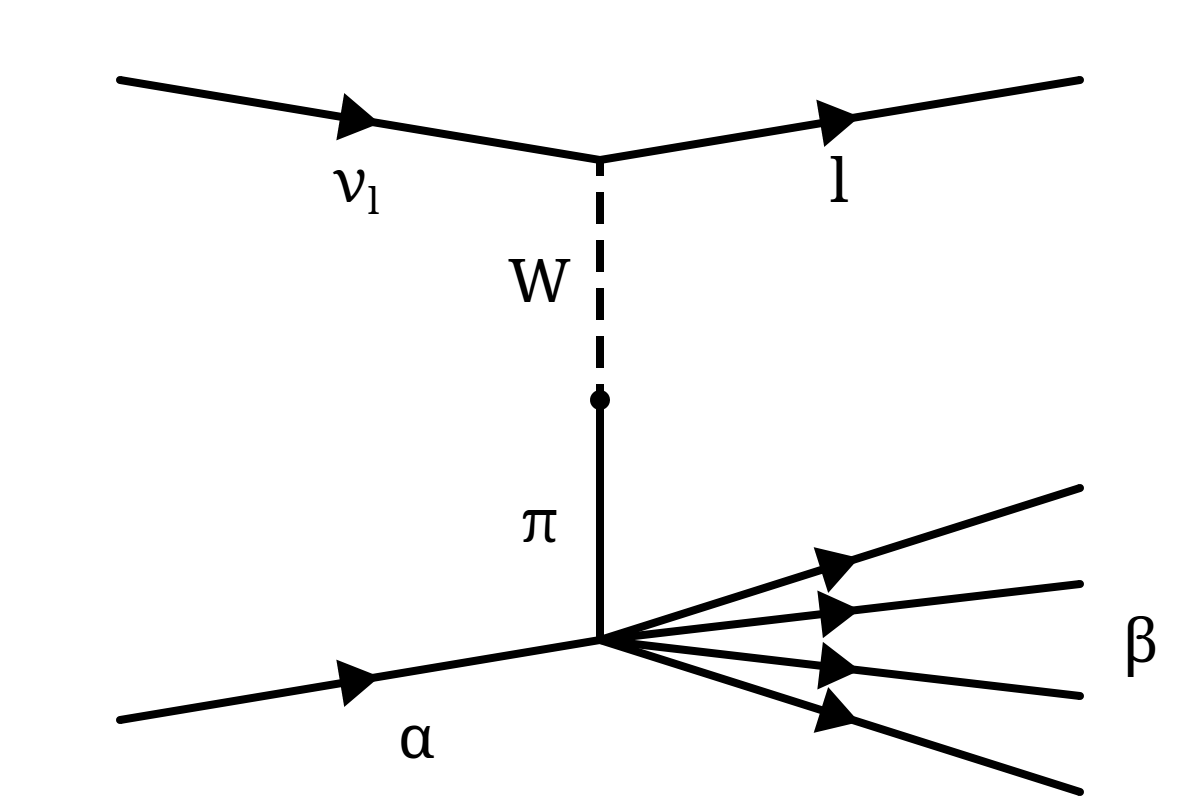
Following the treatment of Adler, this is shown by starting with the amplitude for the process ν_l α → l β:

ℳ = \frac{G_{F}}{\sqrt{2}} {\bar{u}}_{l} (γ_{μ} - γ_{μ} γ_{5}) u_{ν} 〈β | V^{μ} + A^{μ} | α〉

(4.2)

Assuming the final-state lepton emerges parallel to the incoming neutrino and neglecting its mass, the amplitude, squared and averaged over the lepton's spin, is:

〈{|ℳ|}^{2}〉 = 2 {G_{F}}^{2} \frac{E_{ν} E_{l}}{{q_{0}}^{2}} q^{2} {|〈β | V^{μ} + A^{μ} | α〉|}^{2}

(4.3)

〈{|ℳ|}^{2}〉 = 2 {G_{F}}^{2} \frac{E_{ν} E_{l}}{{q_{0}}^{2}} q_{μ} 〈β | V^{μ} + A^{μ} | α〉 q_{ν} {〈β | V^{ν} + A^{ν} | α〉}^{*}

(4.4)

Since q is the four-momentum of the weak current:

〈β | \partial_{μ} (V^{μ} + A^{μ}) | α〉 = q_{μ} 〈β | V^{μ} + A^{μ} | α〉

(4.5)

Substituting Equation 4.5 into Equation 4.4:

〈{|ℳ|}^{2}〉 = 2 {G_{F}}^{2} \frac{E_{ν} E_{l}}{{q_{0}}^{2}} 〈β | \partial_{μ} (V^{μ} + A^{μ}) | α〉 {〈β | \partial_{ν} (V^{ν} + A^{ν}) | α〉}^{*}

(4.6)

〈{|ℳ|}^{2}〉 = 2 {G_{F}}^{2} \frac{E_{ν} E_{l}}{{q_{0}}^{2}} {|〈β | \partial_{μ} (V^{μ} + A^{μ}) | α〉|}^{2}

(4.7)

Requiring the final-state lepton to be parallel to the incoming neutrino is equivalent to requiring a small momentum transfer. Recalling from Section 3.5.1 that at Q² ≈ 0 the vector current is conserved (CVC), implying ∂_μV^μ = 0, leaves just the axial part of the current:

〈{|ℳ|}^{2}〉 = 2 {G_{F}}^{2} \frac{E_{ν} E_{l}}{{q_{0}}^{2}} {|〈β | \partial_{μ} A^{μ} | α〉|}^{2}

(4.8)

This concludes the first step: showing that when a final-state lepton is parallel to the incoming neutrino, the cross-section depends only on the divergence of the axial-vector current.

The divergence of the axial-vector current can be related to another weak process: pion decay. The decay of the pion, which is almost exclusively via π⁺ → μ⁺ ν_μ, is a purely weak process with low-Q² (= m_π²). The matrix element for this process is:

ℳ = \frac{G_{F}}{\sqrt{2}} 〈μ | γ_{μ} - γ_{μ} γ_{5} | ν〉 〈0 | γ_{μ} - γ_{μ} γ_{5} | π〉

(4.9)

The second term, in which the pion field is coupled to the vacuum via the weak current, must be treated with a form-factor since, like nucleons, pions are compound objects which cannot simply be described:

〈0 | V^{μ} + A^{μ} | π〉 = f_{π} {P_{π}}^{μ} Φ

(4.10)

Here Φ is the pion field, P_π is the pion four-momentum, and the form-factor f_π is known as the pion decay constant. Taking the divergence:

〈0 | \partial_{μ} (V^{μ} + A^{μ}) | π〉 = f_{π} {P_{π}}_{μ} {P_{π}}^{μ} Φ

(4.11)

〈0 | \partial_{μ} (V^{μ} + A^{μ}) | π〉 = f_{π} {P_{π}}^{2} Φ

(4.12)

Again, because pion decay is a low-Q² process with CVC, ∂_μV^μ = 0 leaving:

〈0 | \partial_{μ} A^{μ} | π〉 = f_{π} {m_{π}}^{2} Φ

(4.13)

This relates the divergence of the axial-vector current with the pion field and is known as the “PCAC relation” since the fact that m_π ≠ 0 implies that the axial-vector current is not completely conserved. It is through this that the Goldberger-Treiman relation allows the divergence of the axial-vector current in Equation 4.8 can be equated with the corresponding scattering with a pion [17]:

{|〈β | \partial_{μ} A^{μ} | α〉|}^{2} = {f_{π}}^{2} {|ℳ (π + α \to β)|}^{2}

(4.14)

Putting Equation 4.14 into Equation 4.8:

〈{|ℳ|}^{2}〉 = 2 {G_{F}}^{2} \frac{E_{ν} E_{l}}{{q_{0}}^{2}} {f_{π}}^{2} {|ℳ (π + α \to β)|}^{2}

(4.15)

Finally, the corresponding differential cross-section, in terms of Bjorken-x and inelasticity is [18]:

\frac{d^{2} σ}{d x d y} = \frac{{G_{F}}^{2} m_{N} E_{ν}}{π^{2}} {f_{π}}^{2} (1 - y) σ (π + α \to β)

(4.16)

Which is Adler's PCAC theorem, relating the cross-section for neutrino forward-scattering, to the analogous cross-section for pion scattering.

4.2.2. Coherent Pion Production Cross-Section

Adler's PCAC formula is the starting point for the Rein-Sehgal model which was initially authored to describe NC coherent pion production: ν A → ν π⁰ A. Taking Equation 4.16 with α = A and β = π⁰ A, and including the pion scattering cross-section's dependence on |t|, gives a coherent cross-section:

{\frac{d σ}{dx dy d|t|}|}_{Q^{2} = 0} = \frac{{G_{F}}^{2} m_{N} E_{ν}}{π^{2}} {f_{π^{0}}}^{2} (1 - y) \frac{d σ (π^{0} A \to π^{0} A)}{d|t|}

(4.17)

Here, the neutral-pion decay constant f_π⁰² = ½f_π², m_N is the nucleon mass, and the constraint that Q² = 0 comes from the fact that Adler's theorem only applies when the final-state neutrino is scattered exactly forward. They then extrapolated beyond Q² = 0 by including a dipole form-factor:

\frac{d σ}{dx dy d|t|} = \frac{{G_{F}}^{2} m_{N} {f_{π}}^{2} E_{ν} (1 - y)}{2 π^{2}} {(\frac{{M_{A}}^{2}}{{M_{A}}^{2} + Q^{2}})}^{2} \frac{d σ (π^{0} A \to π^{0} A)}{d|t|}

(4.18)

The corresponding cross-section for CC coherent pion production differs by a factor of 2, resulting from the change of pion-decay constant. More recently, in response to the limit set by K2K, Rein and Sehgal published an update to this model [16] to account for the lepton mass in CC interactions. It is implemented as a multiplicative correction, C, to the cross-section in Equation 4.18:

C = {(1 - \frac{½ Q_{min}^{2}}{Q^{2} + m_{π}^{2}})}^{2} + ¼ y \frac{Q_{min}^{2} (Q^{2} - Q_{min}^{2})}{{(Q^{2} + m_{π}^{2})}^{2}}

(4.19)

Where:

Q_{min}^{2} = m_{l}^{2} \frac{y}{1 - y}

(4.20)

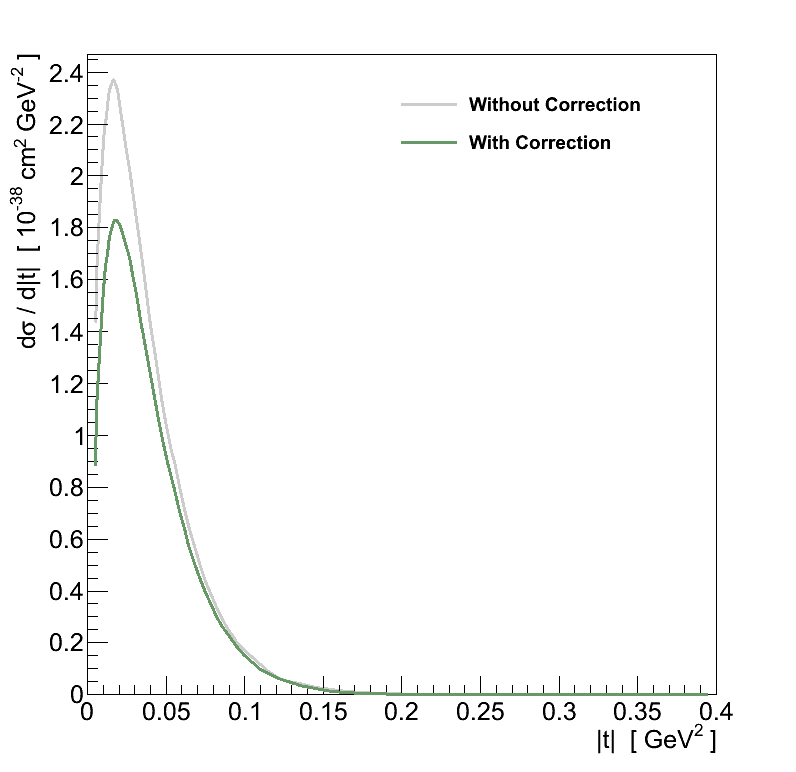
This results in a reduction of the CC coherent cross-section at low energies and, as can be seen in Figure 4.7, there is a dramatic suppression in the Q² distribution at low values. This is significant since both SciBooNE and K2K used the Q² distribution in their search for CC coherent rather than the more characteristic |t|, the shape of which is less affected.

Figure 4.7: The effect of the lepton mass correction term in Equation 4.19 on CC coherent production on ¹²C at E_ν = 1 GeV. The Q² distribution (left) is heavily suppressed at low values, much more so than |t| (right).

4.2.3. Inputs to the Cross-Section

To use this cross-section to make calculations now requires choices to be made about inputs. The most significant of these is the choice of pion scattering cross-section, but there are also three free parameters in the model which can be tweaked.

Rein and Sehgal chose to express the pion-nucleus cross-section in terms of the pion-nucleon forward-scattering cross-section:

\frac{d σ (π^{0} A \to π^{0} A)}{d|t|} = A^{2} {|F_{A} (t)|}^{2} {\frac{d σ (π^{0} N \to π^{0} N)}{d|t|}|}_{t = 0}

(4.21)

Where F_A(t) is a nuclear form-factor. The forward-scattering pion-nucleon cross-section was in turn related to the total cross-section for π⁰-N scattering:

{\frac{d σ (π^{0} N \to π^{0} N)}{d|t|}|}_{t = 0} = \frac{1}{16 π} {(σ_{tot}^{π^{0} N})}^{2} (1 + r^{2})

(4.22)

where r is the ratio of the real to imaginary parts of the π-N forward amplitude:

r = \frac{ℜ [f_{πN} (0)]}{ℑ [f_{πN} (0)]}

(4.23)

Finally, the nucleus form-factor was treated as a |t| dependent exponential, and an absorption factor:

{|F_{A} (t)|}^{2} = e^{- b |t|} F_{abs} = e^{- R_{0} A^{⅓} |t|} F_{abs}

(4.24)

F_{abs} = exp (- \frac{9 A^{⅓}}{16 π {R_{0}}^{2}} σ_{inel}^{π N})

(4.25)

The absorption factor essentially comes from considering the mean path of a pion leaving the nucleus and the probability for it to interact and break coherence. The likelihood of such an interaction is taken from the cross-section for π-N inelastic scattering (the origin of which will also be discussed in a moment), and the nuclear radius scale, R₀, is used to estimate the nuclear radius R = R₀A^⅓.

Putting these elements back into Equation 4.18 gives the Rein-Shegal differential cross-section as:

\frac{d σ}{dx dy d|t|} = \frac{{G_{F}}^{2} m_{N} {f_{π}}^{2} E_{ν} (1 - y)}{2 π^{2}} {(\frac{M_{A}^{2}}{M_{A}^{2} + Q^{2}})}^{2} \frac{A^{2}}{16 π} {(σ_{tot}^{π N})}^{2} (1 + r^{2}) e^{- b |t|} F_{abs}

(4.26)

The most significant input to the Rein-Sehgal model is the choice of total and inelastic pion-nucleon cross-sections. In the original paper, the authors derived them from the corresponding pion-deuterium cross-sections:

σ^{π^{0} N} = \frac{1}{4} (σ^{π^{+} D} + σ^{π^{-} D})

(4.27)

which were parametrised by making line-fits to data from CERN-HERA. The cross-sections implemented in GENIE followed a similar procedure but used more modern π-D data from the Particle Data Group (though the version is not stated). An alternative approach was taken in a standalone implementation of the Rein-Sehgal model for a paper by Berger and Sehgal [19], who took π-proton data from the Particle Data Group (2008) and fitted a superposition of Breit Wigner functions and a term motivated by Regge-theory.

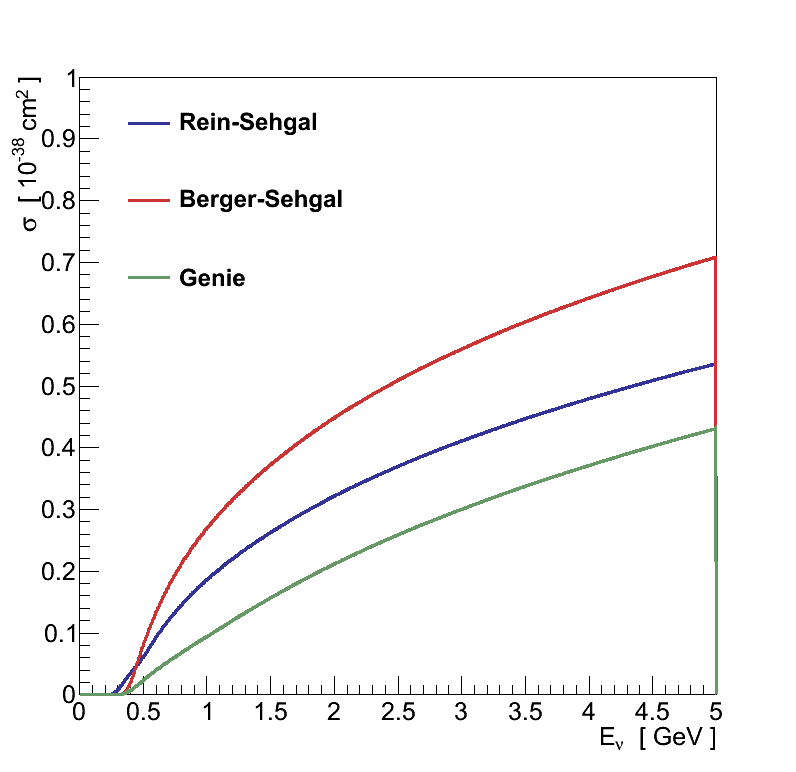
In order to study the effect of these different pion-nucleon cross-sections, without other model differences obscuring, the original Rein-Sehgal and new Berger-Sehgal cross-sections were implemented in a copy of GENIE version 2.6.6. The original Rein-Sehgal cross-sections were implemented utilising the data for them hard-coded within NEUT [20]. The Berger-Sehgal cross-sections were implemented by interfacing with code provided (indirectly) by the authors. Figure 4.8 shows a comparison of these cross-sections. They agree well at high E_π but differ in the amplitude and position of peaks at lower energies. One noticeable difference in the original Rein-Sehgal cross-sections, which is likely to be un-physical, is the continuation of the cross-section down to E_π = 0 - a feature which becomes more significant at lower neutrino energies.

Figure 4.8: Comparison of the total (left) and inelastic (right) π-N cross-sections in the Rein-Sehgal paper and GENIE.

As can be seen in Figure 4.9, these different choices give vastly different total coherent cross-sections, essentially controlled by how high the total, and how low the inelastic, pion-nucleon cross-sections are. More importantly, they strongly affect the pion momentum distribution, which in turn could greatly impact an experiment's sensitivity. Note in particular the difference between the original Rein-Sehgal model (used by K2K and SciBooNE) and the more modern alternatives.

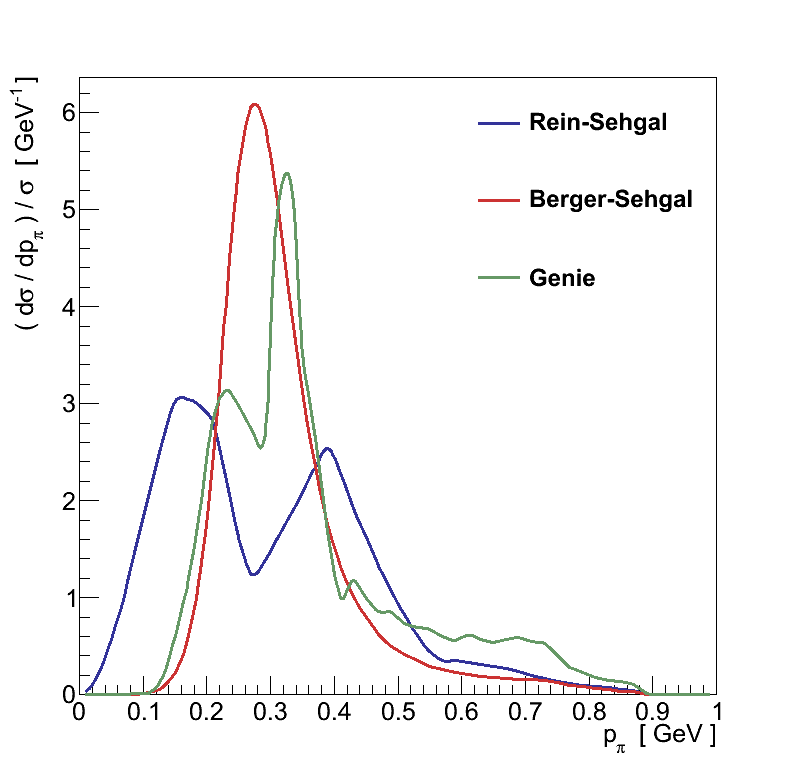
Figure 4.9: The effect of alternative parametrisations of the pion-nucleon cross-sections on the ν_μ CC coherent pion cross-section, and the pion momentum spectrum generated at E_ν = 1.0 GeV, on ¹²C.

The remaining inputs to the model are more simple to evaluate. The axial mass, M_A, mainly scales up the total cross-section, though it does make subtle changes to the shape of dσ/dQ² (Figure 4.10). Since existing coherent pion production data falls far short of being capable of constraining this value, M_A of 1.0 GeV is assumed by all implementations.

Figure 4.10: The effect of M_A on ν_μ CC coherent pion production on ¹²C. The largest effect is on the total cross-section (left), but the normalised Q² distributions at E_ν = 1 GeV (right) show that there is a also a subtle effect on the Q² shape.

Likewise the dominant effect of the nuclear radius scale R₀ (Figure 4.11) is to scale the total cross-section, with larger values of R₀ resulting in smaller cross-sections. However, since it appears in the e^{-R₀A^⅓|t|} term it also affects the shape of the |t| distribution, with higher values of R₀ causing the distribution to peak earlier and drop off faster. Although some past experiments have tried alternative values, the original Rein-Sehgal paper and every significant implementation in current use assumes R₀ to be 1.0 fm.

Figure 4.11: The effect of R₀ on ν_μ CC coherent pion production on ¹²C. The largest effect is on the total cross-section (left), but the |t| distribution at E_ν = 1 GeV (right) is pushed to lower values as R₀ increases.

Finally the value of the ℜ/ℑ ratio, r, exclusively scales the differential cross-section. The value of r was not stated in the original Rein-Sehgal paper and different implementations have taken different approaches. For example, GENIE and NEUGEN take the value to be 0.3, while NEUT and NUANCE have implemented r as a function of E_π. Using the GENIE value of 0.3 implies an increase in the total cross-section of around 10%, which is less than the resolution of the existing data.

Clearly, there can be large variations in the predictions of the Rein-Sehgal model depending on the choice of inputs used, both in the absolute cross-section and in kinematic distributions (particularly of the pion). It is important therefore, recalling Figure 4.5, when making statements about a measurement's compatibility with the Rein-Sehgal model, to keep in mind what version of the model was used in the analysis. However, even if the Rein-Sehgal model can accommodate the low energy data, it is unlikely to be able to do so while simultaneously maintaining compatibility with data at higher energies (Figure 4.4).

This is unsurprising since nuclear effects grow in importance at lower energies. It's questionable whether pion-nucleon cross-sections are appropriate to describe pion-nucleus scattering (Equation 4.27), and certainly any discrepancy in the pion-nucleon cross-sections used will become more significant at lower energies. In addition, the Adler PCAC theorem on which it is based is only valid at Q² ≈ 0, which becomes a less valid approximation as the neutrino's energy becomes comparable in size to the pion mass.

Although it's unclear if the Rein-Sehgal model becomes invalid, and it has yet to be conclusively ruled out, it seems likely that an alternative model will be required to successfully describe coherent pion production at lower neutrino energies.

4.3. Alvarez-Ruso Model

One such alternative is the Alvarez-Ruso model [21] [22] [23]. Unlike the Rein-Sehgal model, which is an example of a “PCAC model”, the Alvarez-Ruso model is an example of a “microscopic model”. Whereas PCAC models describe coherent pion production off of a nucleus in terms of a single interaction channel with that nucleus, a microscopic model describes the process in terms of a coherent sum of neutrino-nucleon interactions where the final-state nucleon is constrained to remain in the same quantum state.

The complete Alvarez-Ruso model includes four such neutrino-nucleon pion producing channels, shown in Figure 4.12, two of which involve the intermediate propagation of a Δ, and two the propagation of a nucleon. The first paper on the model described CC coherent pion production [21] [22], and included only the the s-channel Δ mode which dominates the reaction. This was extended to include the other three modes in the second paper on NC coherent [23], for which they become more relevant.

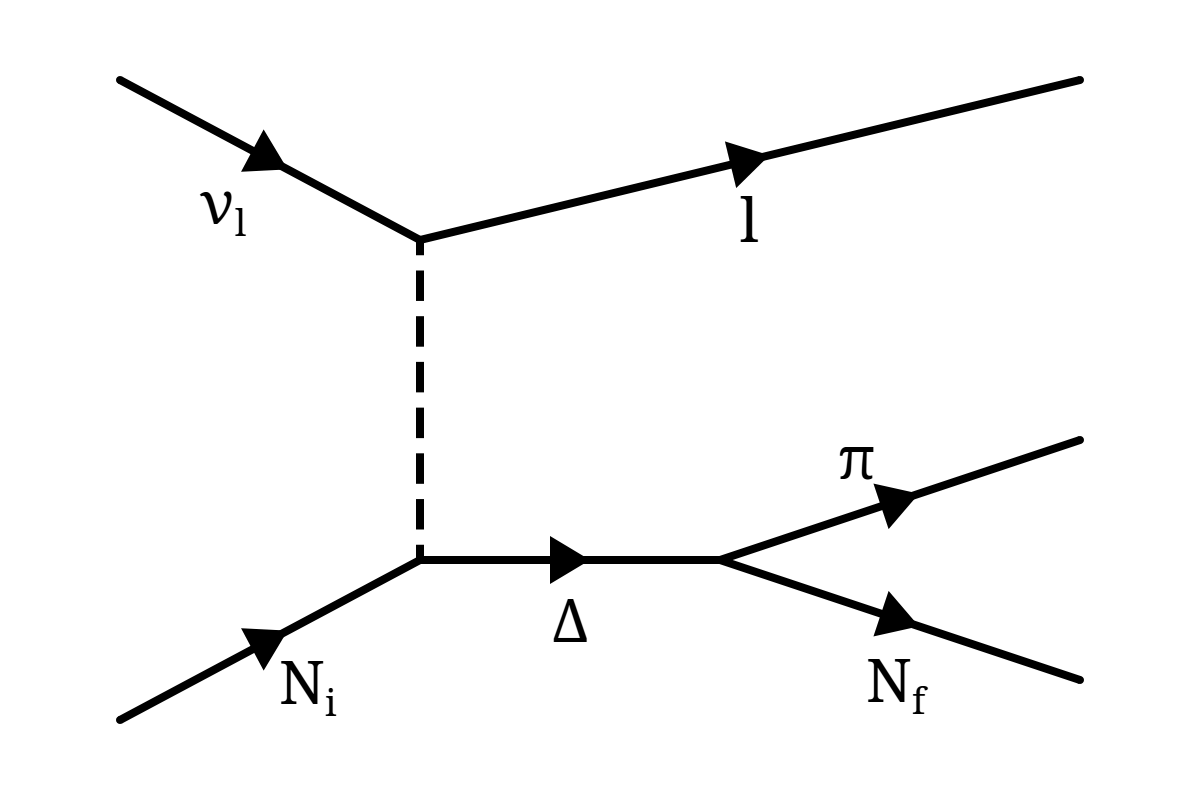
Figure 4.12: Feynman diagrams of the interaction processes which contribute to the Alvarez-Ruso cross-section. The interaction can utilise a Δ (top) or nucleon (bottom) propagator, and proceed via an s-channel (left) or t-channel (right) diagram.

Two significant nuclear effects are also taken into account. First, the properties of Δ's, such as their mass and decay width, are modified by their presence inside a nuclear environment. Second, the outgoing pion is also affected by the nuclear environment, treated as a “distortion” of its wavefunction by a nuclear potential (this is effectively a more careful treatment of the pion absorption included in Rein-Sehgal, Equation 4.25, for low energy pions).

Based on the original papers and code provided by the authors, this Alvarez-Ruso model was implemented in the GENIE neutrino interaction simulation, for the purposes of comparison with the predictions from Rein-Sehgal. While alternative PCAC models have previously been implemented in interaction simulations, this represents the first such implementation of a microscopic model.

We begin by describing the Alvarez-Ruso model in the context of the original s-channel Δ description, then note the differences required for extending it to include all four-channels. The results of the implementation in GENIE are then compared with those from the Rein-Sehgal model, with a focus on the changes in experimental signatures.

4.3.1. The Model

The Alvarez-Ruso coherent pion production cross-section is expressed as a differential in the energy of the outgoing lepton, E_l, and the solid angles of the outgoing lepton and pion, Ω_l and Ω_π:

\frac{d σ}{d E_{l} d Ω_{l} d Ω_{π}} = \frac{1}{8} \frac{|p_{l}| |p_{π}|}{|p_{ν}|} \frac{1}{{(2 π)}^{5}} {|ℳ|}^{2}

(4.28)

The three-momenta p_ν, p_l and p_π are those of the incoming neutrino, and outgoing lepton and pion respectively. Beginning with only the s-channel Δ production mode, the matrix element:

ℳ_{p Δ^{++}} = \sqrt 3 ℳ_{n Δ^{+}} = \sqrt 3 \frac{G_{F}}{\sqrt 2} cos θ_{C} l_{α} J^{α}

(4.29)

is composed of a leptonic current, l_α, and a hadronic current, J^α. The factor √3 difference between the elements for the neutron and proton channels comes from isospin, and θ_C is the usual Cabibbo angle.

The leptonic current is the usual one for leptonic weak interactions:

l_{α} = \bar{u_{l}} (γ_{α} - γ_{α} γ_{5}) u_{ν}

(4.30)

with u_ν and u_l Dirac spinors for the initial neutrino and final-state lepton respectively.

The hadronic current is much more involved, and will be tackled in three steps. Beginning with the basic current for N W → Δ, then extending it to include the Δ decay W N → Δ → Nπ, and modifying the properties of the Δ in the nuclear medium. The distortion of the outgoing pion will be included last.

The basic hadronic current for N W → Δ is:

{J_{Δ}}^{α} = {\bar{ψ}}_{Δ}_{μ} A^{μ α} u_{N,i}

(4.31)

where ψ_Δ is the Rarita-Schwinger spinor 1 for the Δ, u_N,i is the Dirac spinor for the initial nucleon, and as usual for composite particles the N-Δ coupling must be described with the use of form-factors:

\begin{matrix} A^{μ α} = & \{\frac{C_{3}^{V}}{m_{N}} (g^{μ α} γ_{δ} q^{δ} - q^{μ} γ^{α}) + \frac{C_{4}^{V}}{{m_{N}}^{2}} (g^{μ α} q \cdot P_{Δ} - q^{μ} {P_{Δ}}^{α}) + \frac{C_{5}^{V}}{{m_{N}}^{2}} (g^{μ α} q \cdot P_{N,i} - q^{μ} {P_{N,i}}^{α})\} γ_{5} \\ + \{\frac{C_{3}^{A}}{m_{N}} (g^{μ α} γ_{δ} q^{δ} - q^{μ} γ^{α}) + \frac{C_{4}^{A}}{{m_{N}}^{2}} (g^{μ α} q \cdot P_{Δ} - q^{μ} {P_{Δ}}^{α}) + C_{5}^{A} g^{μ α} + \frac{C_{6}^{A}}{{m_{N}}^{2}} q^{μ} q^{α}\} \end{matrix}

(4.32)

The authors draw on various published values for these form-factors which are based on fits to electron and neutrino scattering data.

Equation 4.31 is then extended to cover both the production and decay of the Δ. The hadronic currents for W N → Δ → π N are:

{J_{p π}}^{μ} = \sqrt 3 {J_{n π}}^{μ} = \frac{f^{*}}{m_{π}} {P_{π}}^{α} F (P_{Δ}) {\bar{u}}_{N,f} D (P_{Δ}) Λ_{α β} A^{β μ} u_{N,i}

(4.33)

The currents for the neutron and proton channels differ by a factor √3, again from isospin, giving a total difference between the channels of a factor 3. Λ_αβ is the spin-3/2 projection operator, and the numerical factor f^* = 2.13 is required to reproduce the measured decay width of a free Δ. The Δ-Nπ vertex is described by a form-factor:

F (P_{Δ}) = \frac{λ^{4}}{λ^{4} + {({P_{Δ}}^{2} - {m_{Δ}}^{2})}^{2}}

(4.34)

The value of λ = 1.0 GeV comes from fits to resonance production data in electron and pion scattering.

The Δ propagator, D(P_Δ), is:

D (P_{Δ}) = \frac{1}{(W + m_{Δ}) (W - m_{Δ} + i Γ_{Δ} / 2)}

(4.35)

With W the off-shell Δ's invariant mass, and Γ_Δ(E_Δ) its width. When in a nuclear medium a Δ acquires a self-energy as a consequence of two effects. First, the nucleon from the Δ → N π decay is subject to Pauli-blocking (Section 3.6), reducing its decay width. Second, the potential for the Δ to interact with the surrounding nucleons, e.g. via absorption, affects both its mass and width. The values of m_Δ and Γ_Δ are modified to account for this, using an approach validated on pion, photon and electron scattering [24] [25]. This modification is a function of the local nuclear density, and therefore a function of position in the nucleus, and feeds into Equation 4.35.

Integrating Equation 4.33 coherently over all nucleons, the total hadronic current for the nucleus, A, is:

{J_{Aπ}}^{μ} = \frac{- i}{2} \int e^{i (\vec{q} - p_{π}) \cdot r} (ρ_{p} (r) + \frac{ρ_{n} (r)}{3}) \frac{f^{*}}{m_{π}} {P_{π}}^{α} F (P_{Δ}) D (P_{Δ}) Tr \{{\bar{u}}_{N,f} Λ_{α β} A^{β μ} u_{N,i}\} d^{3} r

(4.36)

where r is the three-vector position in the nucleus, and ρ_n,p are the densities of neutrons and protons. Finally, the effect of the nuclear environment on the outgoing pion is included, by substituting a more realistic wavefunction for the planewave solution used in Equation 4.36:

e^{- i p_{π} \cdot r} \to φ^{*} (p_{π}, r)

(4.37)

This wavefunction can take one of two forms. The full Alvarez-Ruso model calculates φ^* as the solution to the Klein-Gordan equation in an optical potential:

V_{optical} = \frac{Π (r)}{2 E_{π}}

(4.38)

where Π is a pion self-energy which is a function of nucleon density and hence position in the nucleus. This self-energy is calculated using the so called “Δ-hole” model [24], in which pion-nuclear interactions at these energies are dominated by the creation of Δ resonances. While well validated in other scattering fields, the Δ-hole model is only valid for π-N interactions with centre-of-mass energies around the Δ resonance, this limits the Alvarez-Ruso model's validity to E_ν < 3.0 GeV.

However, since solving the Klein-Gordon equation in a potential is a computationally expensive procedure, an alternative “eikonal” approximation was also assessed. Here the pion wavefunction is instead given by:

φ_{eikonal}^{*} = e^{- i p_{π} \cdot r} exp [- i \int_{r}^{\infty} \frac{Π (r')}{2 p_{π}} d r']

(4.39)

using the same pion self-energy, Π, from before. The effect of these two choices is shown in Figure 4.13, for CC interactions on ¹²C at E_ν = 1 GeV. The inclusion of either pion effect reduces the overall cross-section and shifts the pion momentum to lower values, both as a result of the optical potential strongly absorbing pions around the Δ resonance. The simpler eikonal model matches well the more complete Klein-Gordon calculation until p_π drops below around 0.25 GeV.

Figure 4.13: The effect of various nuclear effects on the pion momentum distribution. The red line includes no nuclear effects. The green line includes just the Δ self-energy. The black and blue lines are the full model with the Klein-Gordon and eikonal pion distortions respectively. From [22].

This completes all the ingredients of the model. To add the additional diagram for t-channel Δ production from Figure 4.12, the only substitution required is P_Δ,s = q + P_N,i becomes P_Δ,t = P_N,i - P_π. The corresponding nucleon diagrams require additional changes. Clearly the appropriate masses must be used in Equation 4.34 and Equation 4.35, but no in-medium effects are required. The spin-3/2 projection operator and hadronic matrix are also replaced with:

Λ_{α β} A^{β μ} \to γ_{α} γ_{5} (γ_{δ} {P_{N}}^{δ} + m_{N}) B^{μ}

(4.40)

Where B^μ is the nucleon analogue of A^αμ:

B^{μ} = γ^{μ} F_{1} + \frac{i q_{ν} σ^{μ ν}}{2 m_{N}} F_{2} - γ^{μ} γ_{5} F_{A} - q^{μ} γ_{5} F_{P}

(4.41)

which should be familiar from Equation 3.25 and Equation 3.26. The values for the vector form-factors are taken from fits to electron scattering data [26], F_A takes the usual dipole form with M_A = 1.0 GeV, and PCAC is used to relate it to F_P as in Equation 3.28. The total cross-section is then a coherent sum of the four resulting currents.

When making calculations for the neutral current channel the relevant changes due to the weak couplings need to be accounted for, a factor √2 on the vertices due to the coupling strength, and in the form-factors:

\begin{matrix} C_{i}^{V} \to (1 - 2 {sin}^{2} θ_{W}) C_{i}^{V} \\ F_{i}^{V} \to (1 - 2 {sin}^{2} θ_{W}) F_{i}^{V} \end{matrix}

(4.42)

4.3.2. Comparison with Rein-Sehgal

Utilising the original papers describing this model, the references therein, and the original Fortran implementation developed by the authors, the Alvarez-Ruso model was re-implemented into the GENIE interaction simulation (version 2.6.6).

For the treatment of the outgoing pion distortion the simpler eikonal approximation was used. Computationally, the eikonal approximation is significantly less intensive, which is an important consideration for interaction simulations being utilised in experiments. Although the approximation under-predicts the full calculation at lower pion momenta (Figure 4.13) the shape, which in many respects is more important for experiments, is very similar.

Initially the model was implemented as standalone C++ and validated against the authors' original code. This was then interfaced into the GENIE framework, to enable the generation of events for comparison with GENIE's Rein-Sehgal model. Below, such a comparison is made of their respective predictions for ν_μ induced CC coherent pion production on ¹²C.

Figure 4.14 shows the total cross-sections predicted by both models. The Alvarez-Ruso model gives a lower cross-section than Rein-Sehgal, which is a first requirement to explain the K2K, SciBooNE and MiniBooNE results. The difference becomes increasingly extreme as the energy increases, though this is also where the validity of the Alvarez-Ruso model drops off.

Figure 4.14: Comparison of the total ν_μ CC coherent pion production cross-sections on ¹²C from Rein-Sehgal and Alvarez-Ruso.

The remaining comparisons of the models' differential distributions are all made at E_ν = 1.0 GeV, which is comparable to the energies of many recent and current experiments, and where the Alvarez-Ruso model is completely valid. Figure 4.15 shows the momentum distributions predicted by the two models, which are broadly similar overall. The Alvarez-Ruso model's pion distortion results in a smoother pion momentum distribution than for Rein-Sehgal. It is also slightly softer on average, and if the full Klein-Gordon solution was used for the pion distortion the spectrum would be softer still. This in turn results in a correspondingly smooth, and slightly harder muon momentum spectrum. The double peak structure seen in Rein-Sehgal, as a result of the structure in the pion-nucleon cross-sections, is not reproduced by Alvarez-Ruso which models only one type of pion interaction.

Figure 4.15: Comparison of p_μ (left) and p_π (right) from Rein-Sehgal and Alvarez-Ruso on ¹²C at E_ν = 1.0 GeV.

Figure 4.16 shows the models' angular distributions, the most significant difference being that the pion angular distribution is more forward peaked in the Alvarez-Ruso model. This is also true, to a lesser extent, in the muon angle. One possibility for this difference could be the fact that the Alvarez-Ruso model requires the entire momentum transfer to the nucleus to be absorbed by a single nucleon - which must remain in the same quantum state after the interaction - while Rein-Sehgal allows the entire nucleus to recoil. Reducing the momentum which can be transferred to the nucleus would in turn reduce the scattering angles.

Figure 4.16: Comparison of cosθ_μ (left) and cosθ_π (right) from Rein-Sehgal and Alvarez-Ruso on ¹²C at E_ν = 1.0 GeV.

Finally the |t| distribution, which is the characteristic experimental signature of coherent interactions is shown in Figure 4.17. Predominantly as a result of its more forward-going preference, though also due to its slightly softer pion momentum spectrum, the Alvarez-Ruso model predicts a distribution more sharply peaked at lower values than Rein-Sehgal. It is useful to note that any search for coherent pion production at low |t| developed using Rein-Sehgal would be at least as sensitive to the Alvarez-Ruso model.

Figure 4.17: Comparison of the |t| distributions from Rein-Sehgal and Alvarez-Ruso on ¹²C at E_ν = 1.0 GeV.

4.4. Other Models

Before concluding the chapter a brief comparison with other models is made. This is achieved by utilising data from a recent study [27], comparing alternative neutrino-nucleus interaction models, which made the model predictions gathered publicly available 2.

Figure 4.18 shows the total CC cross-section and pion momentum distributions predicted by these models on ¹²C at E_ν = 1.0 GeV.

Rein-Sehgal, Berger-Sehgal [19], and Schalla-Paschos [28] are all examples of PCAC based models. Amongst other differences, the latter two implement more realistic descriptions of the pion-nucleus interactions. Hernandez [29] and Nakamura [30] are both examples of microscopic models similar to the Alvarez-Ruso model described here.

It was noted in the comparison study, that a large part of the differences in total cross-section could be attributed to different choices of axial-vector form-factors. Even so there are few notable features, either in the total cross-section or pion momentum, which would allow experimental discrimination between the models without precise differential data. However, the comparison study did not gather angular differential cross-sections which in Section 4.3.2 appeared to provide a more discernible difference between the PCAC and microscopic models.

Figure 4.18: Overview of predictions for ν_μ CC coherent pion production on ¹²C. (top) The total cross-section. (bottom) The p_π distribution at E_ν = 1 GeV.

4.5. Summary

Neutrino induced coherent pion production is an important channel for neutrino physics to understand, both because of its potential to be a background in ν_e oscillations and for its integral part in our understanding of total pion production.

The signals seen in high energy experiments show remarkably clear signatures of the process, leaving no doubt of its existence. And the coherent model of Rein-Sehgal matches well those distributions in multiple experiments.

However it has been found across many neutrino-nucleus interaction channels that at low neutrino energies nuclear effects come into play and old assumptions break down. So it is unsurprising that recent low energy searches for coherent pion production reported either limits or significantly reduced cross-sections with respect to Rein-Sehgal.

Nevertheless, it is worth noting that:

K2K reported their CC coherent limit at E_ν ∼ 1.3 GeV using an early version of the model which did not take account of the muon's mass.
Both SciBooNE and K2K searched for CC coherent in the Q² distribution, instead of the more characteristic |t|.
The cross-section and pion kinematics predicted by the Rein-Sehgal model can vary significantly depending on the inputs used.

so it may be premature to completely rule out the Rein-Sehgal model.

Still, difficulty in achieving simultaneous agreement with data at high and low energies, coupled with frailties of Rein-Sehgal at lower energies, suggest an alternative model may be required. One such alternative is the Alvarez-Ruso microscopic model, which was implemented in GENIE. In comparisons with Rein-Sehgal it was found to give a lower cross-section, smoother momentum distributions, and more forward-peaked angular and |t| distributions. There are several other models on offer however, at present, existing experimental data is nowhere near sufficient to discriminate between them.

New data on coherent pion production is necessary. The T2K experiment delivers an intense ν_μ beam through a near detector designed, in part, for neutrino interaction studies. This presents an ideal opportunity to contribute to the understanding of coherent pion production.

Footnotes

The Rarita-Schwinger equation is the spin-3/2 analogue of the spin-1/2 Dirac equation.
To aid comparison, the GENIE and Alvarez-Ruso data from the original study have been replaced with the predictions calculated here.

Contents

1. Introduction

2. Neutrinos & Neutrino Oscillations

3. Neutrino Interactions